高周波誘電加熱の原理
5.数式による誘電体損失の解説

前ページで高周波誘電加熱の熱源となる誘電体損失を図解しましたが、ここでは同じ原理を数式で説明しましょう。

前述したとおり、誘電体損失の発生源は、抵抗の生じる導電電流です。
このとき、誘電体損失、すなわち消費電力 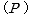は電圧 と導電電流 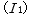の積で求められるので、数式は 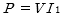となります。
また、導電電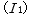流 と合成電流 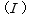との関係を数式で表すと、 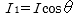となるので、誘電体損失は 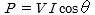と表現できます。

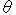はほとんど 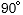に近く（逆に言うと 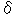は極めて小さな値なので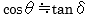）、 として置き換えることができ、 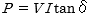となります。
（※一般的に 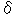が極めて小さいときは、 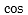は扱いやすい に置き換えられます。）

次に合成電流 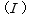を計算してみましょう。
誘電体に流れる導電電流を数式で表すと次のようになります。
導電電流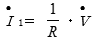
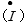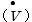電流 は電圧 を抵抗 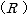で割ったものです。

一方、誘電体に流れる変位電流を数式で表すと次のようになります。
変位電流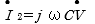
変位電流 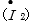は誘電体の静電容量 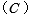と電圧 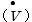の積ですが、静電容量 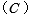は充電時間 に比例するので、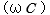 となります。
また、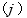 は複素数で、位相が 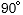進んでいることを表しています。

誘電体に流れる実際の電流は、導電電流と変位電流の和になるので、それを数式で表すと、
合成電流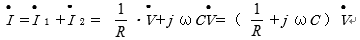
また、静電容量 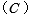は、真空中の静電容量 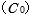と誘電体の比誘電率 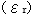の積なので、つまり、 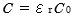なので、合成電流 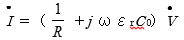となります。
この右辺の 中を 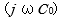で割って外へ出せば、
合成電流 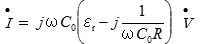となります。

この数式の持つ意味は、次のようになります。

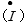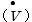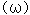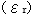誘電体に流れる合成電流 は、電圧 、角周波数 、比誘電率 に比例しますが、このうち、比誘電率 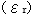はそのまま比例するのではなく、
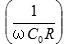だけマイナス（ロス）が発生しています。
このロスが誘電加熱の熱源となる誘電体損失の源です。

さらに、合成電流 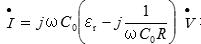を先ほどの誘電体損失 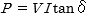に当てはめると
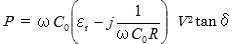となります。
この数式で、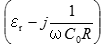 は複素比誘電率といいます。

複素比誘電率の虚数部分の 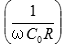は極めて小さい値なので、
誘電比率 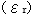と扱っても問題なく、
結果、誘電体損失は 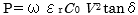の数式が成り立ちます。
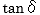のことは誘電体力率（または誘電正接）といいます。

以上のことから、誘電体損失の大きさは、
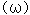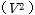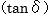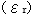角周波数 、電圧の2乗 、誘電体力率 、比誘電率 に比例します。
なお、誘電体力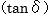率 、比誘電率 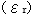は誘電体の種類や温度、周波数によって異なるため、高周波誘電加熱の効率も誘電体の種類や条件によって異なります。