マイクロ波加熱
マイクロ波加熱の可能性を検討する上で重要なものに電力半減深度がある。マイクロ波が誘電体中を浸透しながら吸収され熱に変って減衰していくが、この浸透性を示すものである。図6.3.1にあるように誘電体表面でのマイクロ波電力密度が1/2に半減するまでの深さで、これを電力半減深度Dと称し(6.3.1)式から算出可能である。誘導加熱の「浸透深さ」に当たるものと言える。
D=3.32×107/f*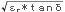 (m) ・・・・・(6.3.1)
(m) ・・・・・(6.3.1)
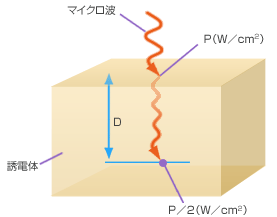
図6.3.1 電力半減深度
一般的にマイクロ波電力による均一加熱度合の限界は(2~2.5)×D程度であり、これ以上厚い物質ではマイクロ波エネルギーが中心部へ到達する前に減衰してしまうため表層と中心部の温度差が大きくなってしまう。この結果、物質の表層と中心部の温度差が大きくなり、均一加熱が困難となる。
興味ある例として、水と氷は同じ分子構造でも液体と固体の状態の損失係数を比べると、次頁図6.3.3 の通り水の方が氷より遥かに大きい。このことはマイクロ波を用い冷凍食品を解凍しようとする場合に、非常に厄介な問題となる。即ち、冷凍食品の一部分が先に溶けて水になると、損失係数が大きくなりマイクロ波は、この水の部分に集中的に吸収され、その部分だけが高温になってしまう、所謂「ランナウエイ加熱」が発生する。本現象は避けるためにはマイクロ波を間欠的に照射して被処理物内部の熱伝導による熱移動を利用するなどの工夫を加えれば、ほぼ均一に解凍可能である。図6.3.2 は水と氷の2450MHzと915MHzの場合の電力半減深度を図示したもので、前者よりも後者の方の電力半減深度が深く、大形の冷凍食品の解凍や大形耐火物の乾燥などに適していることが分かる。
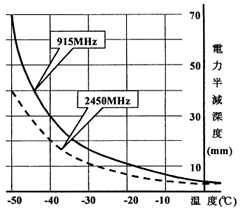
図6.3.2 水と氷の電力半減深度
更に、電子レンジを利用し「湯豆腐、茶碗蒸し」などを加熱調理する場合にも、素材の殆どが水分であることを考慮すると、湯豆腐であれば周囲は加熱されるものの中心部の加熱は甘いとか或いは茶碗蒸であれば中心付近が固まらないというような不具合が発生してしまい、目的の湯豆腐・茶碗蒸しが得られないことがある。これは発振周波数2450MHzを利用している電子レンジが悪いのではなくて、原理的に加熱調理不可能なことを示している。周波数915MHzの電子レンジも考えられるがコスト面で対応困難となる。
尚、周波数2450MHzの場合と915MHzの場合の“物質の比誘電率と誘電体損失角及び電力半減深度Dの関係”を図6.3.3、図6.3.4 に示している。
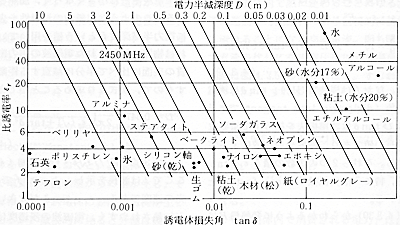
図6.3.3 物質の比誘電率、誘電体損失角、電力半減深度の関係(2450MHz)
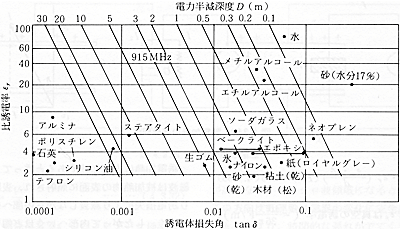
図6.3.4 物質の比誘電率、誘電体損失角、電力半減深度の関係(915MHz)
これらの図から下記のようなことが判る。
① 両図の上辺の浸透深さ(電力半減深度)の目盛を見ると、2450MHzでは「0.01~10m」で915MHzでは「0.1~30m」となっている。電力半減深度の算出式である(6.3.1)式を見ると周波数が分母に入っており、915MHzと2450MHzの比からこのような目盛となっている。
② 図の左下にあるテフロン、石英、ポリスチレン、アルミナ磁器の損失係数は小さいので殆どマイクロ波加熱されず、マイクロ波加熱装置の構造材として利用可能となる。
③ 図の右方にある水、メチルアルコール、ネオプレンなどは損失係数が大きく、マイクロ波加熱され易いものとなり、マイクロ波加熱装置の構造材としては利用不可能となる。
④ 損失係数が大きい同じ材質であっても、ブロック状か…? ペレット状か…? シート状か…?などにより発熱と熱放散のバランスから十分温度上昇しない場合もある。ナイロンなどはブロック状では加熱され温度上昇するが、シート状では放熱が大きく十分温度上昇しないことがある。
⑤ 水の損失係数は、固体か…? 液体か…? によって大幅に変化している。…この損失係数の違いは冷凍食品を解凍する場合に大きな問題となる。即ち、冷凍品のある部位が先に溶けた場合、その部分の損失係数が大きくなり、そこにマイクロ波エネルギーが集中的に吸収されて過熱してしまう所謂「ランナウェイ加熱」が発生することが多い。
電波加熱研究所トップ │ 高周波加熱 技術情報 │ マイクロ波加熱 技術情報 │ 無料で試験いたします │ よくあるご質問
技術情報をさがす 【 業界別でさがす │ 用途別でさがす │ 対象物でさがす │ 技術情報を読む 】