導波管
3.方形及び円形導波管(5)
3-1 方形導波管
(5) 管内波長λg
方形導波管の基本モードの伝送は、一定寸法の導波管内を進行する電波の周波数即ち波長によって、管内を伝播しうるのに必要な入射角が変化して決まってくる。即ち、導波管の両側壁(短辺)に反射した二つの波が合成した波が導波管の管軸に沿って現れるが、導波管の長辺の長さを「a」として、これを利用した管内波長λgの算出式を図10.3.7 、図10.3.8 を利用して導いてみる。
入射波の波長は自由空間波長と同様で図中のλoの間隔である。導波管内の波長即ち管内波長λgは導波管の管軸上の正の波面から次の正の波面までの距離となり、λοとλgの関係は(10.3.4)式の通りとなる。
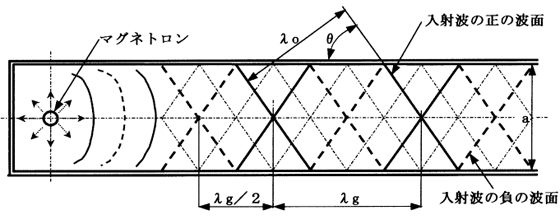
図10.3.7 管内波長の計算図
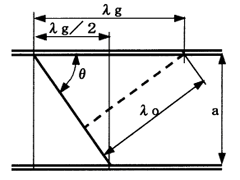
図10.3.8 管内波長の計算図
λο/λg=sinθ ・・・・(10.3.4)
導波管の長辺寸法を「a」とすると(10.3.5)式が得られる。
a/(λg/2)=2*a/λg=tanθ ・・・・(10.3.5)
(10.3.4),(10.3.5)の両式よりλgを消去すると(10.3.6)式となる。
cosθ=λο/(2*a) ・・・・(10.3.6)
即ち、導波管の長辺の寸法aが決まれば、最適入射角が決まることになる。これらの式からθを除去すると(10.3.7)式となる。
λg=λο/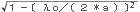
=λο/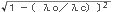 (cm)・・・・(10.3.7)
(cm)・・・・(10.3.7)
遮断周波数fcについて図10.3.9 を参照して説明する。ある電波の周波数が高い時は(波長が短い)、管軸に沿って進む速さが速くなり、従って平面波の通路が短くなる。通路が短かいということは(a)のように一定の距離を進む間での反射の回数が少なくなることである。周波数が低くなると(波長が長い)通路の長さが長くなるため反射の回数が多くなり(b)のようになる。更に、周波数が低くなり遮断周波数に近くなるにつれて、益々反射の回数が多くなり、遮断周波数になると、ついには平面波は(c)のように管壁a-b間で反射して管軸方向に伝播しなくなるイメージとなる。
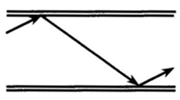
(a)周波数が高い時
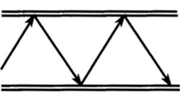
(b)周波数が低い時

(c)周波数がより低い時
図10.3.9 遮断周波数の説明図
電波加熱研究所トップ │ 高周波加熱 技術情報 │ マイクロ波加熱 技術情報 │ 無料で試験いたします │ よくあるご質問
技術情報をさがす 【 業界別でさがす │ 用途別でさがす │ 対象物でさがす │ 技術情報を読む 】